How capacitors work in AC systems
What happens when AC voltage is applied to the capacitor legs? This element behaves differently than a resistor - the resistor allows direct flow of electrons. The current through the resistor is, according to Ohm's law, proportional to the voltage drop across it. In the case of a capacitor, current is drawn in rhythm as the element charges and discharges to a new voltage level.
The capacitor charges up to the voltage applied to it. It acts as a kind of electricity store - as long as a direct voltage (DC) is applied to this element, it maintains its internal charge. When the voltage changes, a current will flow that will try to compensate for the change. The value of the current flowing will be directly proportional to the rate of change of the charge on the capacitor plates.
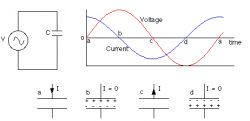
In the figure above, we can see a simple circuit - a capacitor connected to an AC voltage source (top left). In such a system, between the current (blue line) and the voltage (red line) flowing through the capacitor, we observe a phase shift of exactly 90 ° (?? - exactly 1/4 of the entire cycle of alternating voltage; top right).
The AC voltage changes cyclically. The greater the capacity of the connected capacitor, the greater the charge will accumulate between its plates, and thus the greater the current that will flow in the system. It will be similar when we increase the frequency of the alternating voltage - the higher it is, the faster the capacitor must charge, and thus the greater the current flowing in the system. Thus - the current depends on the capacitance of the capacitor and the frequency of the alternating signal.
Capacitive alternating current systems
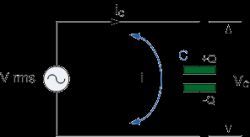
A fully capacitive AC system is one that consists only of an AC voltage source and a capacitor - as shown in the figure above. In this case, a single capacitor is directly connected to the voltage source. As the voltage changes at the source, the capacitor charges and discharges. Current flows through the system all the time - cyclically back and forth. However, no current actually flows through the capacitor. It is the electrons that concentrate first on one of the covers, and then flow through the system and concentrate on the other cover - at no time do they flow through the dielectric separating them, although this may appear to an inexperienced observer.
Capacitor reactance
The flow of electrons through the capacitor is directly proportional to the rate of change of voltage on the plates of this capacitor. Here, the proportionality factor is reactance, just like resistance is the proportionality factor of current and voltage in a system with a resistor.
The reactance is marked with the letter X to distinguish it from the normal resistance for DC voltage (R). However, like the resistance, its unit is the ohm [?]. The following equation describes the dependence of the reactance on the frequency of the alternating signal f (in Hertz) and the capacitance of the capacitor C (expressed in farads).
$$X = \frac {1} {2 \pi f C} = \frac {1} {\omega C}$$
As we can see in the above equation - the higher the frequency or capacity, the smaller the reactance and therefore the greater the current - exactly as described above.
Source: https://www.eeweb.com/profile/andrew-carter/articles/how-capacitors-behave-in-ac-circuits
The capacitor charges up to the voltage applied to it. It acts as a kind of electricity store - as long as a direct voltage (DC) is applied to this element, it maintains its internal charge. When the voltage changes, a current will flow that will try to compensate for the change. The value of the current flowing will be directly proportional to the rate of change of the charge on the capacitor plates.
In the figure above, we can see a simple circuit - a capacitor connected to an AC voltage source (top left). In such a system, between the current (blue line) and the voltage (red line) flowing through the capacitor, we observe a phase shift of exactly 90 ° (?? - exactly 1/4 of the entire cycle of alternating voltage; top right).
The AC voltage changes cyclically. The greater the capacity of the connected capacitor, the greater the charge will accumulate between its plates, and thus the greater the current that will flow in the system. It will be similar when we increase the frequency of the alternating voltage - the higher it is, the faster the capacitor must charge, and thus the greater the current flowing in the system. Thus - the current depends on the capacitance of the capacitor and the frequency of the alternating signal.
Capacitive alternating current systems
A fully capacitive AC system is one that consists only of an AC voltage source and a capacitor - as shown in the figure above. In this case, a single capacitor is directly connected to the voltage source. As the voltage changes at the source, the capacitor charges and discharges. Current flows through the system all the time - cyclically back and forth. However, no current actually flows through the capacitor. It is the electrons that concentrate first on one of the covers, and then flow through the system and concentrate on the other cover - at no time do they flow through the dielectric separating them, although this may appear to an inexperienced observer.
Capacitor reactance
The flow of electrons through the capacitor is directly proportional to the rate of change of voltage on the plates of this capacitor. Here, the proportionality factor is reactance, just like resistance is the proportionality factor of current and voltage in a system with a resistor.
The reactance is marked with the letter X to distinguish it from the normal resistance for DC voltage (R). However, like the resistance, its unit is the ohm [?]. The following equation describes the dependence of the reactance on the frequency of the alternating signal f (in Hertz) and the capacitance of the capacitor C (expressed in farads).
$$X = \frac {1} {2 \pi f C} = \frac {1} {\omega C}$$
As we can see in the above equation - the higher the frequency or capacity, the smaller the reactance and therefore the greater the current - exactly as described above.
Source: https://www.eeweb.com/profile/andrew-carter/articles/how-capacitors-behave-in-ac-circuits



Comments
The article should indicate in bold that not all capacitors are suitable for AC voltage. [Read more]
Brightly . Straight. Affordable. You can ? You can . [Read more]
You have to make up your mind and take one position: ;) First you write that electrons do not flow through the dielectric (i.e., de facto through the capacitor): "It is the electrons [...] that never... [Read more]
The electrons swim (or cycle) to the electrodes and collect there like refugees on the beach. The dielectric, i.e. the border fence, prevents the penetration of electrons (or refugees) to the other side.... [Read more]
Someone above wrote the very truth here, namely that the current flows through the capacitor. And the electrons don't flow? and they do not flow, which does not mean that the current does not flow.... [Read more]
You're right. I agree. Only these equations can be solved and interpreted by a small handful of people. Gradient, divergence, scalar field, vector field, lapsian ... yuck ;-) [Read more]
Fortunately, you don't need to refer to Maxwell's Equations to predict the behavior of a (linear) capacitor. It is enough to take two simple equations: The first equation is a conclusion from... [Read more]
However, not mathematically, it follows directly from the above: the charge exchange on the facings of a capacitor over time is equivalent to the flow of electric current through it. The amount of charge... [Read more]
Even a dielectric is not needed. A vacuum is enough. [Read more]
A vacuum is a dielectric. It is commonly used in RF technology and in vacuum capacitors. [Read more]
Are you sure? Take a look at the definition. A dielectric is a material. A (perfect) vacuum is not a material. Maybe it's a detail, but if we are to be precise, let's be "for the pain". [Read more]
We are one step away from quantum physics ... ;-) [Read more]
Everything is correct. A vacuum is a dielectric with a constant equal to 1. In the material sense, a vacuum is not a dielectric, as it is the term for the complete absence of matter. In the capacitor between... [Read more]
I will write as follows: A capacitor is a specific element. Powered from an "AC" source, it does not itself conduct current through the dielectric, but causes current to flow in the wires connecting it... [Read more]