Hello,
Could you please check if the answers to the questions are right.
Task 1
What is a Wheatstone Bridge for?
A: The Wheatstone bridge, thanks to its structure, enables resistance measurement with high accuracy (from 1 ? to 10 M? . With the help of the three internal resistances of the bridge (knowing their resistance), we can calculate the resistance of the connected element.
. With the help of the three internal resistances of the bridge (knowing their resistance), we can calculate the resistance of the connected element.
Exercise 2
Draw a schematic diagram of the Wheatstone bridge and derive the equation for measuring the resistance with this bridge.
Re: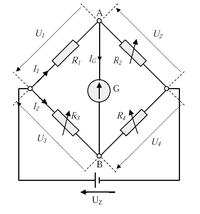
U1 = U3, U2 = U4, U1 = R1 * I1, U2 = R2 * I1, U3 = R3 * I2, U4 = R4 * I2 -> R1 * I1 = R3 * I2, R2 * I1 = R4 * I2 - -> R1 = (R2 * R3) / R4
Exercise 3
Why is this equation not completely accurate and why do we accept this state of affairs?
A: This equation is not complete because the formulas do not take into account the voltage drops on the eight sections of the wires connecting the resistances.
We accept this state of affairs because the inaccuracy is not significant as long as the resistances of the bridge resistors are well above the resistance of the connecting wires.
Task 4
What role does the galvanometer play in the bridge?
A: Magnetoelectric galvanometer (zero detector) (pointer instrument) is used to detect the equilibrium state of the bridge. (After setting which it can be removed from the system).
Task 5
What is the equilibrium state of the sternum and how is this state achieved in practice?
A: The equilibrium state of the bridge is a state in which the potential difference between points A and B becomes zero (the Ig current disappears). This state is achieved by adjusting the resistances R2, R3, R4. This adjustment is called balancing the bridge. Uab = 0
Task 6
Derive the formula for the relative limit error of the resistance measurement with the Wheatstone bridge.
Re:

Task 7
Write a definition of the absolute and relative bridge dead-band error.
A: The absolute bridge insensitivity error ?n is the largest increase in the measured resistance ?R1, at which the galvanometer reading is still equal to zero. This is theoretical.
In practice, it is the increase in the measured resistance ?R1, causing the smallest perceptible displacement of the galvanometer pointer ?a. It is assumed that ?a = 0.1 mm. | ?n | = | ?R1 | when ?a = 0.1mm.
The relative insensitivity error of the bridge ?n is the quotient: | ?n | = | ?n / R1 |.
Task 8
Describe the course of the experimental determination of the insensitivity error.
A: Experimental determination of the insensitivity error requires the realization of increases in the measured resistance R1, which is most often an unregulated element. Therefore, in practice, the equivalent insensitivity error is determined by applying the relative and absolute error to the resistance R3, which is a six-decade laboratory resistor, enabling the implementation of
very small increases in resistance (?R = 0.1? .
.
Task 9
Can I measure a current-dependent (nonlinear) resistance with a Wheatstone bridge?
A: You cannot, because it is used to measure the linear resistance with the knowledge of the parameters of the other linear resistances included in the bridge.
Could you please check if the answers to the questions are right.
Task 1
What is a Wheatstone Bridge for?
A: The Wheatstone bridge, thanks to its structure, enables resistance measurement with high accuracy (from 1 ? to 10 M?
Exercise 2
Draw a schematic diagram of the Wheatstone bridge and derive the equation for measuring the resistance with this bridge.
Re:

U1 = U3, U2 = U4, U1 = R1 * I1, U2 = R2 * I1, U3 = R3 * I2, U4 = R4 * I2 -> R1 * I1 = R3 * I2, R2 * I1 = R4 * I2 - -> R1 = (R2 * R3) / R4
Exercise 3
Why is this equation not completely accurate and why do we accept this state of affairs?
A: This equation is not complete because the formulas do not take into account the voltage drops on the eight sections of the wires connecting the resistances.
We accept this state of affairs because the inaccuracy is not significant as long as the resistances of the bridge resistors are well above the resistance of the connecting wires.
Task 4
What role does the galvanometer play in the bridge?
A: Magnetoelectric galvanometer (zero detector) (pointer instrument) is used to detect the equilibrium state of the bridge. (After setting which it can be removed from the system).
Task 5
What is the equilibrium state of the sternum and how is this state achieved in practice?
A: The equilibrium state of the bridge is a state in which the potential difference between points A and B becomes zero (the Ig current disappears). This state is achieved by adjusting the resistances R2, R3, R4. This adjustment is called balancing the bridge. Uab = 0
Task 6
Derive the formula for the relative limit error of the resistance measurement with the Wheatstone bridge.
Re:

Task 7
Write a definition of the absolute and relative bridge dead-band error.
A: The absolute bridge insensitivity error ?n is the largest increase in the measured resistance ?R1, at which the galvanometer reading is still equal to zero. This is theoretical.
In practice, it is the increase in the measured resistance ?R1, causing the smallest perceptible displacement of the galvanometer pointer ?a. It is assumed that ?a = 0.1 mm. | ?n | = | ?R1 | when ?a = 0.1mm.
The relative insensitivity error of the bridge ?n is the quotient: | ?n | = | ?n / R1 |.
Task 8
Describe the course of the experimental determination of the insensitivity error.
A: Experimental determination of the insensitivity error requires the realization of increases in the measured resistance R1, which is most often an unregulated element. Therefore, in practice, the equivalent insensitivity error is determined by applying the relative and absolute error to the resistance R3, which is a six-decade laboratory resistor, enabling the implementation of
very small increases in resistance (?R = 0.1?
Task 9
Can I measure a current-dependent (nonlinear) resistance with a Wheatstone bridge?
A: You cannot, because it is used to measure the linear resistance with the knowledge of the parameters of the other linear resistances included in the bridge.


