

Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tam
Def. of Logarithms
Logarithm Properties
Polynomials
Quadratic Equation
Common Factoring Examples
Square Root
Absolute Value
Completing the Square
Constant Function
Linear Function
Parabola
Circle
Ellipse
Hyperbola
The basic arithmetic operations are addition, subtraction, multiplication, and division. These operators follow an order of operation.
Addition is the operation of combining two numbers. If more than two numbers are added this can be called summing. Addition is denoted by + symbol. The addition of zero to any number results in the same number. Addition of a negative number is equivalent to subtraction of the absolute value of that number.
Subtraction is the inverse of addition. The subtraction operator will reduce the first operand (minuend) by the second operand (subtrahend). Subtraction is denoted by - symbol.
Multiplication is the product of two numbers and can be considered as a series of repeat addition. Multiplication of a negative number will result in the reciprocal of the number. Multiplication of zero always results in zero. Multiplication of one always results in the same number.
Division is the method to determine the quotient of two numbers. Division is the opposite of multiplication. Division is the dividend divided by the divisor.
The main arithmetic properties are Associative, Commutative, and Distributive. These properties are used to manipulate expressions and to create equivalent expressions in a new form.
The Associative property is related to grouping rules. This rule allows the order of addition or multiplication operation on numbers to be changed and result the same value.

The Commutative property is related the order of operations. This rule applies to both addition and subtraction and allows the operands to change order within the same group.

The law of distribution allows operations in some cases to be broken down into parts. The property is applied when multiplication is applied to a group of division. This law is applied in the case of factoring.



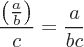
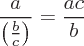

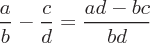

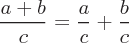
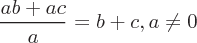



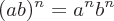


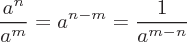

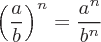



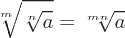

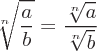







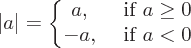





Complex numbers are an extension of the real number system. Complex numbers are defined as a two dimension vector containing a real number and an imaginary number. The imaginary unit is defined as:

The complex number format where a is a real number and b is an imaginary number is defined as:

Unlike the real number system where all numbers are represented on a line, complex numbers are represented on a complex plane, one axis represents real numbers and the other axis represents imaginary numbers.




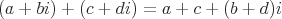



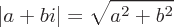


A logarithm is a function that for a specific number returns the power or exponent required to raise a given base to equal that number. Some advantages for using logarithms are very large and very small numbers can be represented with smaller numbers. Another advantage to logarithms is simple addition and subtraction replace equivalent more complex operations. The definition of a logarithms is:
 , where
, where  and
and 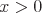
 , where
, where 





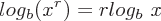
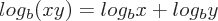

A polynomial is an expression made up of variables, constants and uses the operators addition, subtraction, multiplication, division, and raising to a constant non negative power. Polynomials follow the form:

The polynomial is made up of coefficients multiplied by the variable raised to some integer power. The degree of a polynomial is determined by the largest power the variable is raised.
A quadratic equation is a polynomial of the second order.

The solution of a quadratic equation is the quadratic formula. The quadratic formula is:
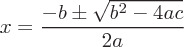
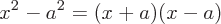

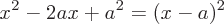
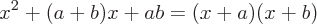




The square root is a function where the square root of a number (x) results in a number (r) that when squared is equal to x.
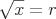 and
and 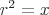
Also the square root property is:
if  then
then 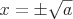
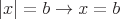 or
or 

 or
or 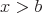
Completing the square is a method used to solve quadratic equations. Algebraic properties are used to manipulate the quadratic polynomial to change its form. This method is one way to derive the quadratic formula.

The steps to complete the square are:
Expressions evaluated at incremental points then plotted on a Cartesian coordinate system is a plot or graph.
When a function is equal to a constant, for all values of x, f(x) is equal to the constant. The graph of this function is a straight line through the point (0,c).

A linear function follows the form:

The graph of this function has a slope of m and the y intercept is b. It passes through the point (0,b). The slope is defined as:
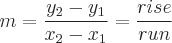
An addition form for linear functions is the point slope form:

A parabola is a graphical representation of a quadratic function.

The graph of a parabola in this form opens up if a>0 and opens down if a<0. The vertex of the parabola is located at:
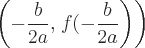
Other forms of parabolas are:
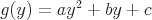
The graph of a parabola in this form opens right if a>0 or opens left if a<0. The vertex of the parabola is located
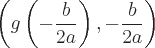
The function of a circle follows the form:

Where the center of the circle is (h,k) and the radius of the circle is r.
The function of an ellipse follows the form:

Where the center of the ellipse is (h,k)
The function of a Hyperbola that opens right and left from the center follows the form:
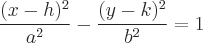
The function of a Hyperbola that opens up and down from the center follows the form:
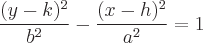
Where the center of the hyperbola is (h,k), with asymptotes that pass through the center with slopes of:
