

Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tam
In trigonometry, the law of sines, also known as the Sine Rule, is very useful for solving problems with triangles, since it works for any shape of triangle.
![]()
The law of cosines, also known as the Cosine Rule, allows us to solve the missing parts of a triangle when two sides and the angle between them is known.
a2 = b2 + c2 – 2bc cosα
b2 = a2 + c2 – 2ac cosβ
c2 = a2 + b2 – 2ab cosγ
Note that a, b and c all represent the three sides of the triangle, while γ represents the known internal angle.
The law of tangents, also known as the Tangent Rule, defines the relationship between the length of the opposing sides and the tangents of two internal angles of a triangle.
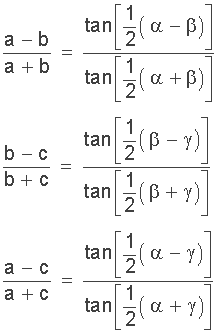
For trigonometry laws, Mollweide’s formula is an equation that defines the relationship between three sides and the angles of a triangle, and can be used to double-check the previous trigonometry laws of a triangle.
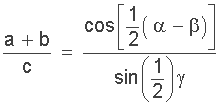
Identities for the tangent and cotangent functions can be derived from similar formulas used for the sine and cosine functions. The identity for tangents is given as follows:
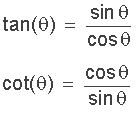
The reciprocal identities rule is basically definitions of the reciprocals of the three previous trigonometric ratios and as such are important trigonometric identities we can use to solve various trigonometry problems.
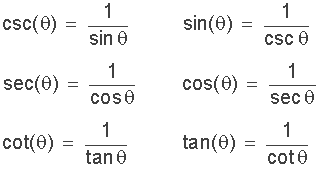
As its name suggests, Pythagorean Identities are derived from the standard Pythagoras theorem for right-angled triangles.
sin2θ + cos2θ = 1
tan2θ + 1 = sec2θ
cot2θ + 1 = csc2θ
Trigonometric even and odd, or odd and even identities, show whether each trigonometric function is an odd function or an even function.
sin(–θ) = –sin(θ)
cos(–θ) = cos(θ)
tan(–θ) = –tan(θ)
csc(–θ) = –csc(θ)
sec(–θ) = sec(θ)
cot(–θ) = –cot(θ)
A periodic function is a function that constantly repeats itself at regular intervals over time, such as the sine function. When plotted onto a graph, the shape of a periodic function is symmetrical, repeating itself along the horizontal X-axis. Sinusoidal waveforms are periodic functions.
sin(θ + 2πn) = sin(θ)
cos(θ + 2πn) = cos(θ)
tan(θ + πn) = tan(θ)
csc(θ + 2πn) = csc(θ)
sec(θ + 2πn) = sec(θ)
cot(θ + πn) = cot(θ)
For the cosine double angle identity, there are three forms of the identity we can create from the basic form, cos(2α) = cos2(α) – sin2(α) using Pythagorean Identity.
sin(2θ) = 2sinθcosθ
cos(2θ) = cos2θ – sin2θ = 2cos2θ – 1 = 1 – 2sin2θ
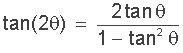
As the name suggests, half angle identities or functions have half angles in them. Note that the ± sign simply means that the square root result can be positive or negative in value depending on which quadrant the angle lies in.
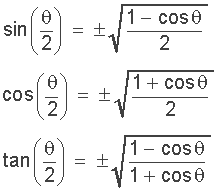
In trigonometry, the sum and difference identities are used to find the value of a trigonometric function at a specific angle in terms of two angles which have known trigonometric values. For example, 75o = 60o + 15o.
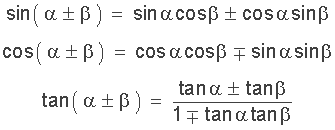
A product to sum identity can be used to depict the product of the sine and cosine functions as a sum. The product to sum identity is based on the previous sum and difference identities used in trigonometry.
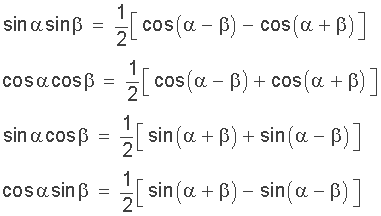
The sum to product identity is used to express the sum and difference of sines and cosines as products of their sine and cosine functions. That is, it can express the difference of a sine function to the difference of a cosine function as the summed product of these two functions.
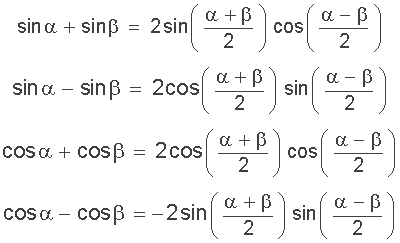
Cofunction identities show the relationship between the different complementary angles and the trigonometric functions that exist between the sine and cosine, tangent and cotangent, and secant and cosecant pairs. We can use the angle sum property of a right-angled triangle to derive the six cofunction identities.
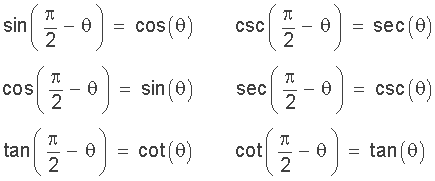
We have seen here in this Trigonometry Laws and Identities tutorial that these trigonometric laws and rules are very useful in the solving of triangles using the values relating to its sides and angles.
We have also seen that there are clear relationships for tangent, cotangent, secant, and cosecant expressions in terms of sine and cosine, making these identities useful in real life situations. Note that the Pythagorean formula for the laws of sines and cosines is one of the most important trigonometry laws and identities used for electrical and electronics engineering.