It is best to consider the integration and differentiation system together and start with the differentiation system because it is an inverse operation of integration and simpler to understand.
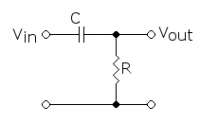
This system gives the higher output voltage, the faster the input voltage changes. For example, let's take a potentiometer connected to a constant voltage working as a position sensor, connect the differential system to the potentiometer slider and we have a signal proportional to the speed of movement of the object mechanically connected to the potentiometer, simple and useful.
Integration is the reverse operation, let's assume that we install a tachometric generator in the car giving voltage proportional to the speed, integrating the speed we get information about the distance traveled, integration is a simplification of the summation, in the end the way can also be counted by adding up the sections traveled by the car at different speeds.
In practice, such simple passive systems are rarely used to perform mathematical operations from which they have a name, because neither the integral nor differentiating system is ideal, but with the use of active elements it is possible to make systems closer to the ideal.
The integrity of the integrity system is not ideal, it means that the ideal system after providing a constant value signal should give the output a constantly increasing voltage - indefinitely if necessary, the "integrating" RC system will give the output at most as much as it has at the input, a perfect integration system from a rectangular course will do a triangular with a constant slope, and a passive system will do a "folded triangle" as below
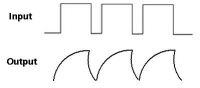
The waveform is closer to the triangle, the lower the output amplitude in relation to the input one, so the possibilities of improving the system's operation are weak, because what is almost perfect if the amplitude is extremely small.
The integrating system connected after the differentiator or vice versa should give the same course as at the input.



