What does the value of the rectified voltage depend on and how to calculate it?

Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tamRadek18 wrote:I solved it by limiting the ripple voltage to about 1V with a current consumption of 15A. I used capacitors with a capacity of 130 mF and I will say that the ripple voltage was eliminated to the minimum possible.
b00gie wrote:It will work in power supplies with tube rectifiers, not with Si diodes.In tube amplifier systems, it is recommended to use a factor of 1.26 (determined empirically) instead of 1.41.
Source:
http://www.mif.pg.gda.pl/homepages/tom/zasilacz.htm

kariak97 wrote:So before rectification we have power P = 230^2/R, and after rectification P = 322^2/R, we just doubled the power of the current that comes out of the socket simply by rectifying it.
jony wrote:Have you calculated the current drawn from the socket?
kariak97 wrote:I know it's calculated correctly, I just don't understand why the output is more powerful than the input.
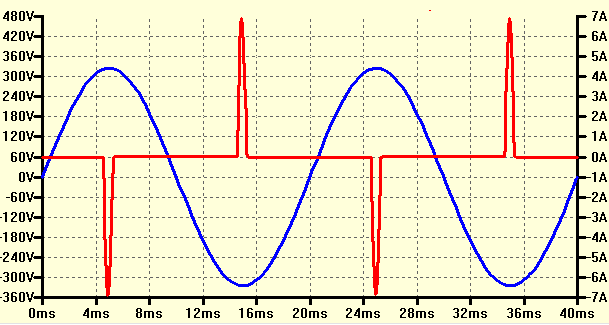
kariak97 wrote:It seems logical to me (yes, I know that I think wrong, but I haven't found any information about it anywhere) that if the AC voltage at the input works (from the energy point of view) like 230V DC, then at the output of the rectifier with a filter it should be 230 - 1.2 V (drop on diodes).
