Optimizing Electric Motor Performance: PID Control Techniques Explained
When we're looking into drones, balance boards, smart cars, and inverted pendulums, there's this term that keeps popping up - PID. But what on earth is PID and what's it for? Well, in this piece, I made a simple motor controller to dig into the principle of PID and figure out how to use it right.

First off, we need to make clear the goals of the experiment. That is, I need to be able to make my motor turn to any angle. And while it's rotating, it has to stay steady and not have any shakes or wobbles.
Motor Selection
To complete this experiment, the microcontroller has to control the motor really precisely and get details like the motor's speed and position from it. So, a direct current motor with an encoder is required. The micro-controller can get the speed and position info of the motor through the encoder. The encoder motors you can buy on the market usually fall into Hall or optical encoders. Here, I have chosen a TT encoder motor with a reduction ratio of 120 from DFRobot.

According to the data manual provided on the official website, his encoder can output 16 pulse signals per revolution. After passing through the gearbox, the output shaft can output a total of 16 * 120 = 1920 pulse signals for one complete rotation.

The motor purchased comes with a total of six wires. The four on the left side are for the encoder, while the two on the right side are for the motor itself.

Motor Driver Chip
For the motor driver chip, I picked the L293D(Link), which is a dual-channel H-bridge brushed motor driver. With just two input pins and an enable pin, you can control the forward and reverse direction of a motor as well as its speed adjustment.

Micro-controller
The micro-controller utilizes the STM32F103C8T6(Link) series core board, which is available for purchase on Taobao. For this particular micro-controller, its timer can handle encoder signal input. So, all we have to do is hook up the motor's encoder output pins to the timer's encoder input pins. That way, the timer can count the signals automatically.

The high-performance STM32 microcontroller from Unikeyic (Link) component platform is the core element in this motor control system. Its excellent processing ability and rich peripheral resources ensure the stable operation of the entire system. You can find this amazing product available for purchase online on Unikeyic component platform.
After preparing these materials, I designed a circuit diagram.
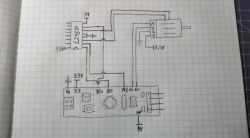
According to this circuit diagram, I have successfully soldered the circuit onto a perforated board.

Here, the entire circuit part has been completed. Next up is the software part.
PID Controller
The name of the PID controller actually explains its basic principle. PID stands for three words: Proportion, Integration, and Differential. In Chinese, this translates to Proportional, Integral, and Derivative controllers. As shown in the figure below:
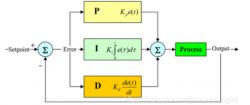
In this setup, the leftmost part is the input for the PID controller, and the rightmost part is its output. We can see an arrow going from the output back to the sum accumulator on the input side with a negative sign. This indicates that the PID controller uses negative feedback. At this moment, the error signal is just the difference between the input and output signals. To put it simply, taking our experimental goal as an example, if the motor rotates too much, the PID controller will make it go back to the original angle.
After passing through the accumulator, the error signal is divided into three parts: proportional operation, integral operation, and derivative operation. The proportional operation directly multiplies the error signal by the Kp value, in the integral operation, each time the error is integrated and then multiplied by the Ki value, and in the derivative operation, it is the derivative of the error signal multiplied by the Kd value. Kp, Ki, and Kd are all constants, and we need to adjust these three different parameters according to various systems. I will now explain from a mathematical perspective how each operation contributes to the output.
When the error signal is big, the P term responds actively to the output and contributes the largest value, making it the main part of the output at that moment. When the error signal is changing rapidly, the derivative operation of the D term will make a significant contribution to the output. The I term acts as a corrector. When there are small errors that accumulate in the system over time, the I term will correct these errors.
In general, the core of the PID controller lies in these three operational processes. In this experiment, if I want to control the motor to rotate to a specific angle, my input will be the desired angle of rotation. After being processed by the PID controller, it will output a PWM value to control the motor movement, and at the same time, the encoder keeps providing feedback on the current position. Through continuous calculations with the PID controller, the motor can quickly and stably rotate to the specified angle.
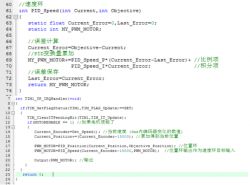
Implementation of the Code
It is worth noting that for the three operation formulas mentioned in the PID structure diagram above (proportional, derivative, and integral), they all operate on continuous signals. For a micro-controller, it's clearly not possible to deal with continuous signals. A practical way is to run the PID algorithm at set intervals. So, for the discrete position PID algorithm, its formula is like this:
For the three variables, their calculation methods are as follows:
So, the next step is to implement the entire program. Since the micro-controller board I am using does not have a serial communication chip, it is not conducive to later debugging, so I am using an inherent USB interface of the STM32 to simulate serial port communication. Next, create a new STM32 project and add the related peripheral initialization code (motor encoder, etc.).
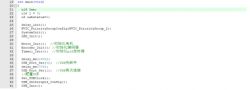
Next, I have written a PID calculation function based on the formula mentioned above.
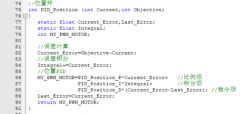
To run the PID algorithm regularly, I've set up a timer with a precision of 5 milliseconds. This enables the PID algorithm to be executed each time the timer's interrupt is activated. From inside the timer's interrupt function, we can see that the processing involves feeding the current position and the target position into the PID calculator, getting its output, and then sending it to the motor control function for execution.

And in the output control function of the motor, the content is as follows:
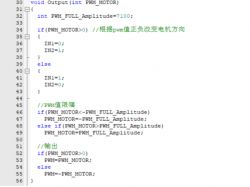
Control the rotation direction of the motor through the value output by the PID controller, then limit the range of the PID output values, and finally assign them to the PWM generator.
Experiment
Let's start the experiment. At first, we'll set the I and D parameters of the PID controller to zero, and assign a small value to Kp. After that, we'll compile the project and then flash it onto the STM32.
Power on the STM32. If the STM32 is using a USB-emulated serial port, software installation will be needed. I'll include the relevant details at the end of the document. Open the serial port debugging assistant, type 'h' and then press the Enter key, and click Send. The help information will be printed out. You can see the supported commands, such as reading the encoder position, modifying PID parameters, and rotating left and right, etc.
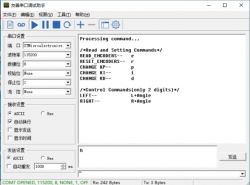
Next, in the serial port debugging assistant, send "L90" and press Enter. Then observe the motor rotating 90 degrees. However, note that the motor has some wobble and the response speed is relatively slow.
After that, gradually increase the Kp value until the wobble amplitude decreases and the motor's response speed gradually rises. When vibrations near the target position are noticed, start increasing the Kd value to suppress these vibrations. When the Kp value is adjusted to 500 and the Kd value to 900, the motor's wobble situation improves significantly, as shown in the video.
Although the vibration issue is resolved, after several rotations, the motor's error gradually emerges, as shown in the figure below. After a full rotation, it fails to return to the original point.
So next, I increased the Ki value. But it's recommended not to increase the Ki value too much, usually within a range of a few tenths of a unit. Here, I set the Ki value to 0.01 to correct the error generated after each rotation.
With this, the basic adjustment of the PID parameters is almost completed, and the motor can execute my instructions very well.
Improvement
I've noticed that when the rotation angle is set to a large value, the motor rotates at full speed first and then gradually slows down until it reaches the set position. This leads to a problem: when the motor is running at full speed, the duty cycle of the PWM (Pulse Width Modulation) is 100%, which means the motor is effectively directly connected to the power supply. At this moment, we have no control over the motor's speed. So, if there is any instability in the power supply voltage, the motor speed will inevitably fluctuate, resulting in unstable rotation. This is definitely not the result I want. Therefore, it's necessary to introduce a speed control loop in such cases.
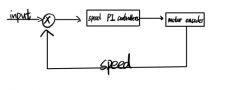
Because of the natural inertia in an electric motor's rotation, its speed can't change suddenly. So, I've only put PI control in the velocity loop controller. This controller is used to adjust the motor's speed while it's rotating and will be nested inside the position loop controller. The final implementation code is as follows: