Understanding 1/3 Period Phase Shift in 50Hz Three-Phase Electrical Systems

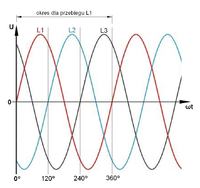
Hello, perhaps a trivial question, but what does a phase shift of 1/3 period mean?
I`m a layman in this topic, but I understand it like this:

The current has a frequency of 50Hz, if I understand correctly, this refers to voltage changes, and 50Hz means 50 voltage increases and decreases per second, so the period is 0.02 seconds.

Does this mean that changes in individual phases have the same frequency, but are not synchronized, but shifted in time by 0.02/3 seconds?

Hello.
Buddy Luckey13, you explained it very confusingly, but it looks like you understand it well.

Below I have drawn a graph with voltage waveforms for three phases L1, L2 and L3. It shows very well what is going on.
As you can see, the individual phases L1, L2 and L3 are shifted by an angle of 120°. Shifting by an angle of 120° is your 0.02/3s.
I also marked the period for the L1 phase. The situation is similar for phases L2 and L3.


Regards.

Convoluted, because I had virtually no knowledge on the subject
Out of curiosity, I have one more question: if the voltage oscillates at a frequency of 50Hz, what is 230V voltage?
From what I found, the voltage oscillates from 325 to -325V, the average in such a case would be 0, so where does the 230V come from?

Hello.

Luckey13 wrote:

...if the voltage oscillates at a frequency of 50Hz, what is 230V voltage?
From what I found, the voltage oscillates from 325 to -325V, the average in such a case would be 0, so where does the 230V come from?

Yes, the voltage oscillates in the range of approximately 325V to -325V, and the voltage of 230V is the effective value of this alternating voltage. The average value is indeed 0, but the average and effective value are not the same. In simple terms, the effective value is as if the lower half-periods of the waveform were transferred (reflected) to the upper part of the graph, and then the average was taken.
For sinusoidal waveforms, the maximum voltage value is equal to √2 times the effective value. Hence √2*230V≈325V.

More precisely, the effective value is the value of the direct voltage, the application of which to the resistor will cause a current to flow in it and, as a result, the release of thermal power exactly the same as the application of an alternating voltage of such an effective value to the same resistor.
Regards.

Rysio4001 wrote:

In simple terms, the effective value is as if the lower half-periods of the waveform were transferred (reflected) to the upper part of the graph, and only then the average was taken

No, this is the average with modulus.
The effective value is as if you multiplied your sine by itself and then took the average from it. Why? Because the power is P = U * I, I = U/R, so assuming we have some constant load R => P = U^2/R, so the power is proportional to the square of the voltage. Since our voltage is not constant, but alternating, we need some measure to determine it. Why do we take an average? I explained why in a square above

Thank you for helping me understand