Some time ago, I acquired a very interesting sensor, the BH1790GLC (Link) heart rate sensor. This sensor is manufactured by ROHM, a Japanese company.

As a hardware dev designer, the first thing I do when I get this module is to go to the official website and download its datasheet. Looking at the datasheet helps me figure out what this sensor is like.
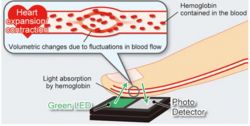
When a pulse signal is sent out, it makes the volume of the blood vessels change, like what's shown in the picture above. The sensor picks up the pulse by catching these changes in the blood vessels.
The full sensor block diagram is like this:
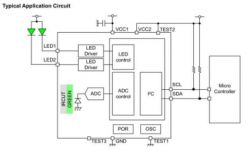
The sensor requires the connection of two green LED beads. Ordinary LEDs won't suffice; the module uses the SML-M13MT (Link) model. The special thing about this LED compared to normal ones is that it can get an even spread of light intensity in a certain range by using reflection.
For high - quality LED components like the SML-M13MT and a wide range of electronic parts, check out Unikeyic (Link) component platform, available for purchase online.
Inside the chip, there's a driving circuit for the green LED. What's more, outside the sensor, there's a set of IRCUT filters. These filters block out external and infrared light, making sure that only green light can pass through the IRCUT and get to the ADC for collection. In the end, the data is sent out via IIC.
The whole sensor doesn't really need a lot of components. But I've looked into it, and this module is actually quite expensive. The online price quotes are around 100.
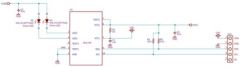
The circuit diagram of the module is like this:
I won't go into detail about the other parameters; you can refer to the sensor's datasheet for more information.
There are only a handful of registers in the whole sensor. Besides the ID register, there are just control registers. The data that's collected is stored in two groups of data registers: DATOUT_LEDON and DATOUT_OFF.
The manual also has measurement control instructions. These instructions keep me from getting all mixed up.

According to this timing sequence, I configured the 0x41 – 0x43 registers as follows.

Finally, following the sequential requirements, the values of DATOUT_LEDON and DATOUT_OFF were read.
Then I printed the read values of DATOUT_LEDON and DATOUT_OFF through the serial port and plotted them.

The figure below shows the data waveform when my finger is not placed on it: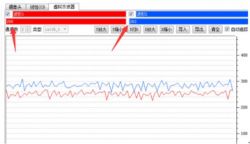
The values of DATAOUT_LEDOFF (red) and DATAOUT_LEDON (blue) remain almost stable, with indoor data hovering around 260.
When a finger is placed on the sensor, the waveform changes immediately.
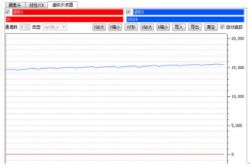
DATAOUT_LEDOFF (red) immediately goes down to around 20, while DATAOUT_LEDON (in blue) has an obvious fluctuation. The range of this fluctuation is really small, and the value of DATAOUT_LEDON (blue) keeps rising steadily.
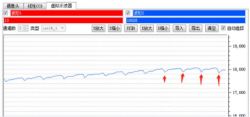
To extract pulse data from such a waveform, an appropriate algorithm is indeed needed.
An IIR (Infinite Impulse Response) filter seems to be a good choice. When considering IIR filters, it's also necessary to mention FIR (Finite Impulse Response) filters since both are types of digital linear filters. The main distinctions between them are as follows:
Under the same technical specifications, IIR filters, thanks to their feedback from output to input, demand fewer parameters and consume fewer resources compared to FIR filters.
FIR filters are capable of achieving strict linear phase, which is something IIR filters can't do.
IIR filters can be designed as standard low-pass, high-pass, band-pass, band-stop, or all-pass filters. On the other hand, FIR filters offer much greater flexibility and can be designed to carry out ideal orthogonal transformations, ideal differentiation, linear modulation, and so on.
Consequently, in our specific application, just considering an IIR filter is enough as the phase shift isn't an issue for us.
For the waveform described above, when a finger presses down, both low-pass and high-pass filtering are required. The normal pulse range for humans is between 60 - 100 beats per minute. Taking extreme cases into account, we'll set the low-pass filter at 3.5 Hz and the high-pass filter at 0.5 Hz. This way, we'll only capture signals within the 0.5 Hz - 3.5 Hz range.
Let’s first discuss the IIR filter. Here, I have chosen a Direct Form I IIR filter, implemented through a cascade of second-order biquads. Each biquad consists of a second-order filter:
[ y[n] = b_0 \cdot x[n] + b_1 \cdot x[n-1] + b_2 \cdot x[n-2] + a_1 \cdot y[n-1] + a_2 \cdot y[n-2] ]
The Direct Form I algorithm requires 5 coefficients and 4 state variables for each stage, as illustrated below.
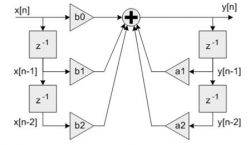
x[n] represents the input variable, while y[n] is the output value after applying the IIR filter.
According to this formula, a first-order IIR filter can be realized. By cascading several such filters, you can achieve a higher-order IIR filter.
The formula is established, but how do we determine the parameters b0, b1, b2, a1, and a2 in the formula?
The answer is: by using MATLAB.
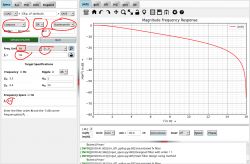
Open the filter design toolbox with fdatool.
Set the filter parameters:
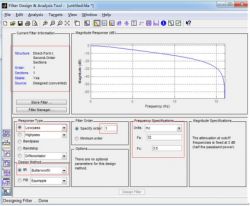
Please note that the BH1790GLC (Link) heart rate sensor we have configured outputs data at 32Hz, hence the sampling frequency of the filter is 32Hz with a cutoff frequency of 3.5Hz.
The filter parameters as output by MATLAB are as follows:
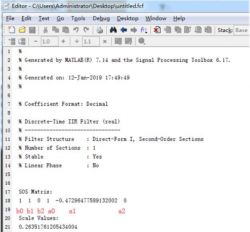
Having obtained the parameters for the filter, let's commence coding.
Define the structure for IIR filter parameters:
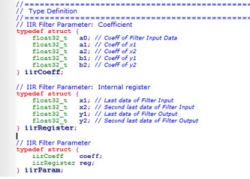
Initialization of IIR Filter

The code implementation for calculating the IIR filter is as follows:
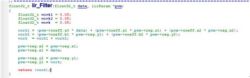
Regarding the section on filters, that's basically the gist of it.
The remaining part involves using an IIR filter.
The program reads the sensor data at a frequency of 32Hz.
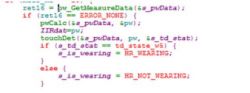
pw_GetMeasureData(&s_pwData); retrieves the sensor data and stores it in s_pwData.
pwCalc(&s_pwData, &pw); The data undergoes IIR filtering to obtain PW data.
The filtering method is as follows:
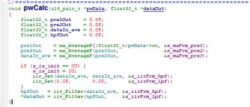
First of all, the raw data goes through a moving average smoothing process. After that, it passes through a high-pass filter and then a low-pass filter. In the end, it gives us the output dataOut.
Now, I'll send both the raw data and the filtered data through the serial port. The waveform will be shown like this:
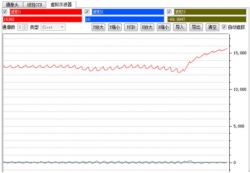
Red for DATAOUT_LEDON, blue for DATAOUT_LEDOFF, and green for data after IIR filtering
After magnifying the PW waveform:
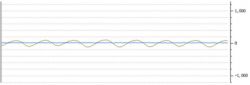
After the IIR filtering process, it can be noticed that pw nearly shows a regular sinusoidal wave. This makes it extremely convenient to precisely measure the pulse heartbeat that the sensor has detected.
The final heartbeat statistics are presented through the serial port in the following way:
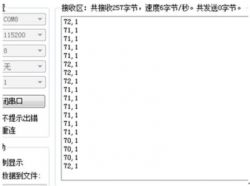

As a hardware dev designer, the first thing I do when I get this module is to go to the official website and download its datasheet. Looking at the datasheet helps me figure out what this sensor is like.

When a pulse signal is sent out, it makes the volume of the blood vessels change, like what's shown in the picture above. The sensor picks up the pulse by catching these changes in the blood vessels.
The full sensor block diagram is like this:

The sensor requires the connection of two green LED beads. Ordinary LEDs won't suffice; the module uses the SML-M13MT (Link) model. The special thing about this LED compared to normal ones is that it can get an even spread of light intensity in a certain range by using reflection.
For high - quality LED components like the SML-M13MT and a wide range of electronic parts, check out Unikeyic (Link) component platform, available for purchase online.
Inside the chip, there's a driving circuit for the green LED. What's more, outside the sensor, there's a set of IRCUT filters. These filters block out external and infrared light, making sure that only green light can pass through the IRCUT and get to the ADC for collection. In the end, the data is sent out via IIC.
The whole sensor doesn't really need a lot of components. But I've looked into it, and this module is actually quite expensive. The online price quotes are around 100.
The circuit diagram of the module is like this:

I won't go into detail about the other parameters; you can refer to the sensor's datasheet for more information.
There are only a handful of registers in the whole sensor. Besides the ID register, there are just control registers. The data that's collected is stored in two groups of data registers: DATOUT_LEDON and DATOUT_OFF.
The manual also has measurement control instructions. These instructions keep me from getting all mixed up.

According to this timing sequence, I configured the 0x41 – 0x43 registers as follows.

Finally, following the sequential requirements, the values of DATOUT_LEDON and DATOUT_OFF were read.
Then I printed the read values of DATOUT_LEDON and DATOUT_OFF through the serial port and plotted them.
The figure below shows the data waveform when my finger is not placed on it:

The values of DATAOUT_LEDOFF (red) and DATAOUT_LEDON (blue) remain almost stable, with indoor data hovering around 260.
When a finger is placed on the sensor, the waveform changes immediately.

DATAOUT_LEDOFF (red) immediately goes down to around 20, while DATAOUT_LEDON (in blue) has an obvious fluctuation. The range of this fluctuation is really small, and the value of DATAOUT_LEDON (blue) keeps rising steadily.

To extract pulse data from such a waveform, an appropriate algorithm is indeed needed.
An IIR (Infinite Impulse Response) filter seems to be a good choice. When considering IIR filters, it's also necessary to mention FIR (Finite Impulse Response) filters since both are types of digital linear filters. The main distinctions between them are as follows:
Under the same technical specifications, IIR filters, thanks to their feedback from output to input, demand fewer parameters and consume fewer resources compared to FIR filters.
FIR filters are capable of achieving strict linear phase, which is something IIR filters can't do.
IIR filters can be designed as standard low-pass, high-pass, band-pass, band-stop, or all-pass filters. On the other hand, FIR filters offer much greater flexibility and can be designed to carry out ideal orthogonal transformations, ideal differentiation, linear modulation, and so on.
Consequently, in our specific application, just considering an IIR filter is enough as the phase shift isn't an issue for us.
For the waveform described above, when a finger presses down, both low-pass and high-pass filtering are required. The normal pulse range for humans is between 60 - 100 beats per minute. Taking extreme cases into account, we'll set the low-pass filter at 3.5 Hz and the high-pass filter at 0.5 Hz. This way, we'll only capture signals within the 0.5 Hz - 3.5 Hz range.
Let’s first discuss the IIR filter. Here, I have chosen a Direct Form I IIR filter, implemented through a cascade of second-order biquads. Each biquad consists of a second-order filter:
[ y[n] = b_0 \cdot x[n] + b_1 \cdot x[n-1] + b_2 \cdot x[n-2] + a_1 \cdot y[n-1] + a_2 \cdot y[n-2] ]
The Direct Form I algorithm requires 5 coefficients and 4 state variables for each stage, as illustrated below.

x[n] represents the input variable, while y[n] is the output value after applying the IIR filter.
According to this formula, a first-order IIR filter can be realized. By cascading several such filters, you can achieve a higher-order IIR filter.

The formula is established, but how do we determine the parameters b0, b1, b2, a1, and a2 in the formula?
The answer is: by using MATLAB.
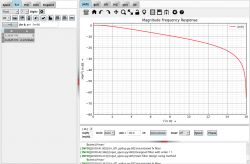
Open the filter design toolbox with fdatool.

Set the filter parameters:

Please note that the BH1790GLC (Link) heart rate sensor we have configured outputs data at 32Hz, hence the sampling frequency of the filter is 32Hz with a cutoff frequency of 3.5Hz.
The filter parameters as output by MATLAB are as follows:

Having obtained the parameters for the filter, let's commence coding.
Define the structure for IIR filter parameters:

Initialization of IIR Filter

The code implementation for calculating the IIR filter is as follows:

Regarding the section on filters, that's basically the gist of it.
The remaining part involves using an IIR filter.
The program reads the sensor data at a frequency of 32Hz.

pw_GetMeasureData(&s_pwData); retrieves the sensor data and stores it in s_pwData.
pwCalc(&s_pwData, &pw); The data undergoes IIR filtering to obtain PW data.
The filtering method is as follows:

First of all, the raw data goes through a moving average smoothing process. After that, it passes through a high-pass filter and then a low-pass filter. In the end, it gives us the output dataOut.
Now, I'll send both the raw data and the filtered data through the serial port. The waveform will be shown like this:

Red for DATAOUT_LEDON, blue for DATAOUT_LEDOFF, and green for data after IIR filtering
After magnifying the PW waveform:

After the IIR filtering process, it can be noticed that pw nearly shows a regular sinusoidal wave. This makes it extremely convenient to precisely measure the pulse heartbeat that the sensor has detected.
The final heartbeat statistics are presented through the serial port in the following way: