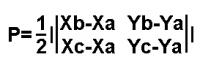Formula for the area of a triangle in the xy coordinate system

Question

Some of you know this pattern. I used to have it in junior high school, but I can't find it, and I need it very much
I have the coordinates of the vertices:
A = (5.3)
B = (10.4)
C = (2.8)
I am asking for this pattern
thanks

Tdv · Answer

Using the method of the engineer Nachamow, the field for Ci should be 15.5, but the pattern I took and a long time ago ...

Anonymous · Answer

I don't remember either, because I went to gymnasium right after the war. But this is a product (I think an scalar) of two vectors defined by the sides of the triangle and a half, something like (X1 * Y2 + X2 * Y1) / 2 if that reminds you of something, (X1, Y1) is a vector - the side of the triangle.

elektryk · Answer

Heron's formula:
P = [p * (pa) * (pb) * (pc)] ^ (1/2) (to the 1/2 power it is actually a square root but I can't write it) p is half the circumference p = (a + b + c) / 2
Knowing the coordinates of the vertices, I think you will be able to calculate the lengths of the sides (a, b, c)

Anonymous · Answer

If you calculate, write how much you got, because I'm also curious (I have a similar problem). :? : x 8O

lipek86 · Answer

yes, I know heron's pattern only I know how to count the lengths of the sides on the basis of coordinates. Enlighten me because somehow I don't have the strength to think. :? :cry: is there any pattern for that ??? because as I now rozrysowłam it, I thought that it could be done with your Pythagoras.

elektryk · Answer

the length of the segment is the root of the sum of the squares of the coordinate difference (I hope I was right), it looks something like this v [(x1-x2) ^ 2 + (y1-y2) ^ 2]

Leap · Answer

if two coordinates then root [(y1-y2) ^ 2 + (x1-x2) ^ 2] e.g. for A (5,3) and B (10,4) y1 = 5, x1 = 3 y2 = 10, x2 = 4 we substitute and we get the square root of 26 that is | AB | = 5, piece

lipek86 · Answer

That's right. I did it on tw. Pythagoras (I drew a layout xy) and the sides come out element 26 square root 80 square root 34 then I think I can do it

Leap · Answer

and so, just like that, the area is counted with the help of determinants you do a 2 by 3 matrix and put the coordinates there and count

Gorgoroth · Answer

The area of the triangle is generally 0.5 * a * h. Let's assume that "a" will be episode | AB | so you count the length of the section about the ends in points (5,3) and (10,4)

AB= sqr (x2-x1)^2 + (y2-y1)^2

The length | AB | comes out = sqr26
now you count the height "h" which is the distance of point C from the straight line passing through points A and B. So first you calculate the equation of the line passing through A and B

y-y1 = (y2-y1) / (x2-x1)  * (x-x1)

So we have an equation of a simple figure

y = x - 20

Now you find the distance of point C (2,8) from this line

h = Ax0 + By0 + C / sqr (A^2 + B^2)

Above you have the formula for the distance of the point C = (x0; y0) from the line Ax + By + C = 0.
From this formula the distance of this point is 5 sqr 2.
So you have all the data:
a = sqr26
h = 5sqr2
So the area is ~ 18 square units
And that's all

elektryk · Answer

I wonder how the determinant of a non-square matrix counts.

Owsik · Answer

It is also possible to calculate from the formula given in the appendix by substituting the coordinates of the points

candle · Answer

almost (x1 * y2-x2 * y1) / 2 ... I consider the subject as exhausted .. heron's formula is for people with too much time candle

Formula for the area of a triangle in the xy coordinate system

Post #1

Post #2

Post #3

Post #4

Post #5

Post #6

Post #7

Post #8

Post #9

Post #10

Post #11

Post #12

Post #13

Post #14

Topic summary